本系列文章配套代码获取有以下两种途径:
-
通过百度网盘获取:
链接:https://pan.baidu.com/s/1jG-rGG4QMuZu0t0kEEl7SA?pwd=mnsj提取码:mnsj
-
前往GitHub获取:
https://github.com/returu/Data_Visualization散点图使用笛卡尔坐标系,将每个数据点绘制在x轴和y轴的交叉位置上,是数据分析和可视化中最常用的图表类型之一。通过观察点的分布,能够直观地展示两个变量之间的关系,例如可以判断两个变量之间是否存在相关性,是正相关还是负相关,以及相关性的强度。
函数语法:
plt.scatter(x, y, s=None, c=None, *, marker=None, cmap=None,norm=None, vmin=None, vmax=None, alpha=None,linewidths=None, edgecolors=None, colorizer=None,plotnonfinite=False, data=None, **kwargs)
-
必需参数:
-
大小与颜色:
-
标记样式:
-
颜色映射:
-
其他参数:
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize
# 设置中文字体
plt.rcParams['font.sans-serif']=['SimHei']
#显示负号
matplotlib.rcParams['axes.unicode_minus']=False
# 生成示例数据
np.random.seed(42) # 设置随机种子,确保结果可复现
n_points = 100 # 数据点数量
# 生成基础数据
x = np.random.randn(n_points) # x轴数据(正态分布)
y = 2 * x + np.random.randn(n_points) # y轴数据(与x相关)
# 生成用于演示不同参数的数据
sizes = np.random.randint(50, 500, n_points) # 点的大小(50-500之间的随机值)
colors = x.copy() # 颜色值(取决于x的值)
# 添加一些特殊值(NaN、inf)用于演示plotnonfinite参数
#
colors[5] = np.nan # NaN
colors[15] = np.inf # 正无穷
colors[25] = -np.inf # 负无穷
# 准备数据框用于演示data参数
data = {
'x_data': x,
'y_data': y
}
# 创建自定义规范化器,在创建时指定vmin和vmax,而不是在scatter函数中
custom_norm = Normalize(vmin=-1, vmax=1) # 在这里设置vmin和vmax
# 创建图形和轴
fig, ax = plt.subplots(figsize=(10, 7))
# 使用scatter函数绘制散点图
scatter = ax.scatter(
# 主要数据参数
x='x_data', # x轴数据,使用data参数中的键名
y='y_data', # y轴数据,使用data参数中的键名
s=sizes, # 点的大小
c=colors, # 点的颜色
# 标记样式参数
marker='*', # 点的形状(星形)
# 颜色映射参数
cmap='hsv', # 颜色映射方案
norm=custom_norm, # 自定义规范化器,已包含vmin和vmax
# 透明度和边缘参数
alpha=0.8, # 点的透明度
linewidths=1, # 点边缘线宽
edgecolors='black', # 点边缘颜色
# 特殊值处理参数
plotnonfinite=True, # 绘制包含无穷大和NaN的值
# 数据来源参数
data=data, # 数据来源,允许x和y使用键名
# 其他关键字参数(**kwargs)
label='数据点', # 标签,用于图例
)
# 添加颜色条以显示颜色映射
cbar = plt.colorbar(scatter, ax=ax)
cbar.set_label('颜色值')
# 添加图例、标题和轴标签
ax.legend()
ax.set_title('scatter()函数所有参数使用示例(包含特殊值处理)', fontsize=14)
ax.set_xlabel('X轴', fontsize=12)
ax.set_ylabel('Y轴', fontsize=12)
# 添加网格
ax.grid(True, linestyle='--', alpha=0.7)
# 显示图形
plt.tight_layout()
plt.show()
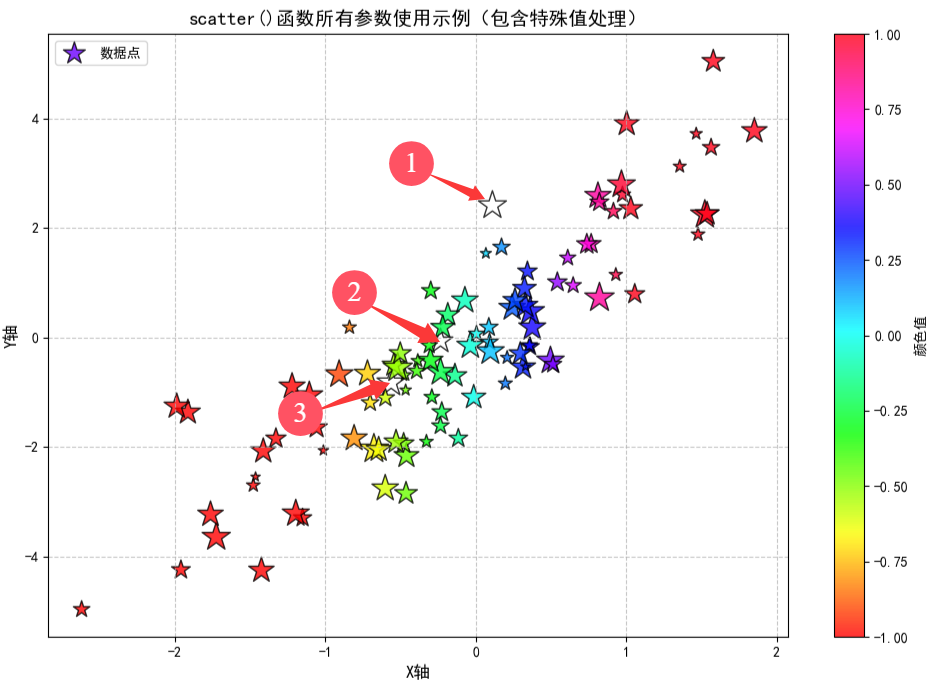
使用示例:
import pandas as pd
# 从网络加载原始Iris数据集
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
column_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class']
# 读取数据
df = pd.read_csv(url, header=None, names=column_names)
-
示例 1:利用颜色编码引入第三维度
通过为散点赋予不同颜色,可引入分类或连续型第三变量。例如,使用连续色阶表示数值大小,或采用离散色调区分类别。该方法在保持二维分布结构的同时,增强了图表的信息密度,适用于多变量数据的可视化比较。
plt.figure(figsize=(6, 4))
scatter = plt.scatter(
df['sepal_length'],
df['sepal_width'],
c=df['petal_length'], # 第三维度
cmap='viridis',
s=80,
edgecolors='k',
linewidths=.5,
vmin=df['petal_length'].min(),
vmax=df['petal_length'].max()
)
cbar = plt.colorbar(scatter , label='Petal Length (cm)')
plt.title("Iris: Sepal vs Petal Length (color)")
plt.xlabel("Sepal Length (cm)")
plt.ylabel("Sepal Width (cm)")
plt.show()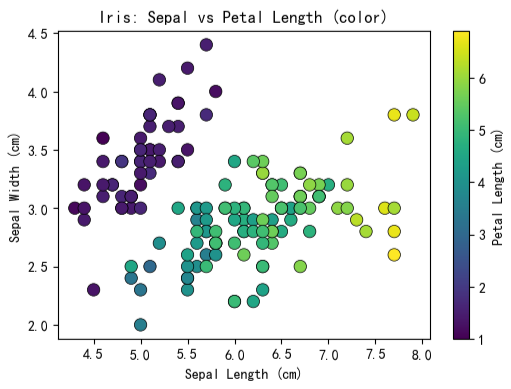
-
示例 2:通过点大小编码第四维度
在颜色映射基础上,可通过调节散点尺寸进一步表示第四维连续变量。较大的点可对应较高数值,该方法尤其适用于强调某些观测值在额外维度上的差异,但需注意避免视觉重叠与认知负荷过高。
plt.figure(figsize=(8, 6))
# 计算点的大小范围,使大小差异更明显
min_size = 50
max_size = 500
size_range = max_size - min_size
petal_width_min = df['petal_width'].min()
petal_width_max = df['petal_width'].max()
# 将花瓣宽度映射到点大小
point_sizes = min_size + size_range * (df['petal_width'] - petal_width_min) / (petal_width_max - petal_width_min)
scatter = plt.scatter(
df['sepal_length'],
df['sepal_width'],
c=df['petal_length'], # 第三维度:颜色表示花瓣长度
s=point_sizes, # 第四维度:大小表示花瓣宽度
cmap='viridis',
alpha=0.7, # 添加透明度以便更好地看到重叠的点
edgecolors='k',
linewidths=.5,
vmin=df['petal_length'].min(),
vmax=df['petal_length'].max()
)
# 添加颜色条
cbar = plt.colorbar(scatter, label='Petal Length (cm)')
# 创建图例显示花瓣宽度与点大小的关系
# 选择几个代表性的花瓣宽度值
width_values = [0.1, 1.0, 2.0]
legend_sizes = [min_size + size_range * (w - petal_width_min) / (petal_width_max - petal_width_min) for w in width_values]
# 创建图例
legend_elements = []
for w, s in zip(width_values, legend_sizes):
legend_elements.append(plt.scatter([], [], s=s, edgecolors='k', linewidths=0.5,
color='gray', alpha=0.7, label=f'{w} cm'))
# 添加图例
legend = plt.legend(handles=legend_elements, loc='upper right', title='Petal Width',
frameon=True, framealpha=0.8)
plt.title("Sepal Dimensions with Petal Length (color) and Width (size)")
plt.xlabel("Sepal Length (cm)")
plt.ylabel("Sepal Width (cm)")
# 添加网格以便更好地读取坐标
plt.grid(True, linestyle='--', alpha=0.3)
plt.tight_layout()
plt.show()
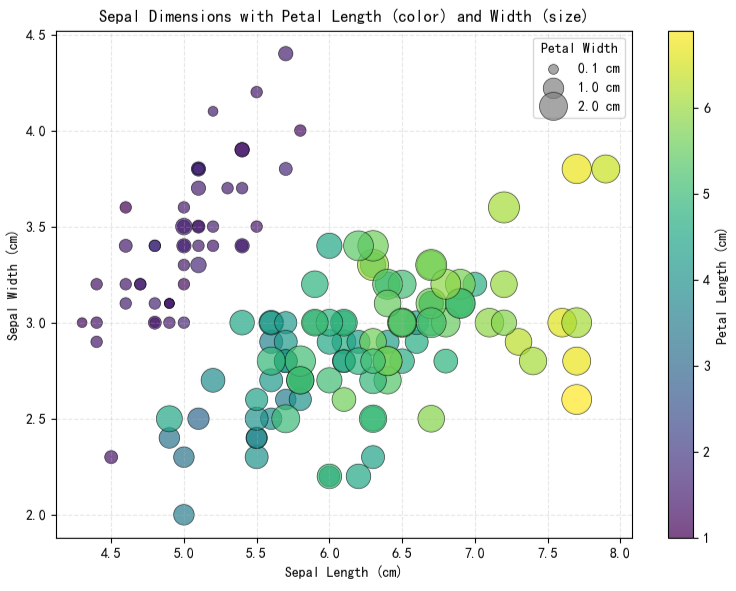
-
示例 3:添加回归线以揭示趋势关系
引入线性或非线性回归线可清晰展示变量间的统计关系趋势,辅助识别相关性、异常值及模型拟合情况。建议同时提供拟合方程与判定系数(R²),以增强结果的可解释性与科学性。
from sklearn.linear_model import LinearRegression
plt.figure(figsize=(8, 6))
# 创建散点图
scatter = plt.scatter(
df['sepal_length'],
df['sepal_width'],
c=df['petal_length'], # 第三维度
cmap='viridis',
s=80,
edgecolors='k',
linewidths=.5,
vmin=df['petal_length'].min(),
vmax=df['petal_length'].max()
)
# 添加线性回归线
# 准备数据
X = df['sepal_length'].values.reshape(-1, 1)
y = df['sepal_width'].values
# 创建并训练线性回归模型
model = LinearRegression()
model.fit(X, y)
# 生成预测值
x_range = np.linspace(df['sepal_length'].min(), df['sepal_length'].max(), 100)
y_pred = model.predict(x_range.reshape(-1, 1))
# 绘制回归线
plt.plot(x_range, y_pred, color='red', linewidth=2,
label=f'线性回归: y = {model.coef_[0]:.2f}x + {model.intercept_:.2f}')
# 添加颜色条
cbar = plt.colorbar(scatter, label='Petal Length (cm)')
# 添加图例
plt.legend(loc='upper right')
plt.title("Iris: Sepal Dimensions with Linear Regression")
plt.xlabel("Sepal Length (cm)")
plt.ylabel("Sepal Width (cm)")
# 添加网格
plt.grid(True, linestyle='--', alpha=0.3)
# 显示R²值
r_squared = model.score(X, y)
plt.text(0.05, 0.95, f'R$^2$ = {r_squared:.3f}', transform=plt.gca().transAxes,
bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.8))
plt.show()
可视化结果如下图所示:
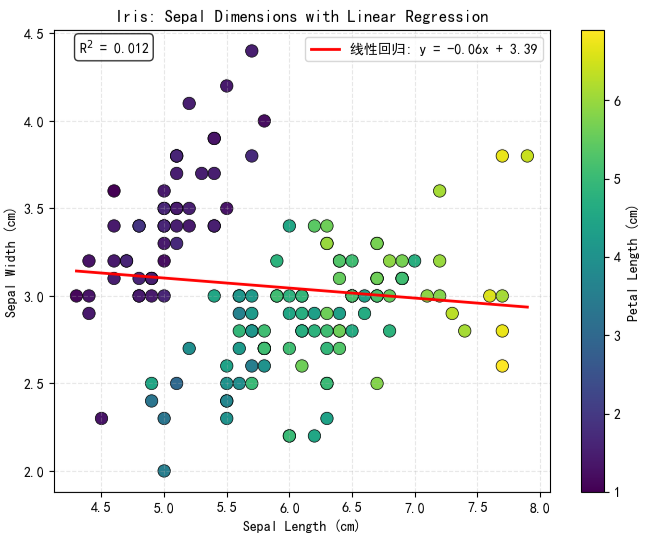
-
示例 4:创建带有边际分布的散点图
联合分布图可在散点图周围添加变量的直方图或核密度估计。该结构同时展示了双变量关系与单变量分布,适用于全面描述数据的统计特征。
-
使用matplotlib:
matplotlib 需手动划分画布,主区域画散点图,侧边用直方图呈现单个变量分布。
from matplotlib.gridspec import GridSpec
from matplotlib.patches import Patch
# 把三种鸢尾花映射成 0/1/2
labels, unique = np.unique(df['class'], return_inverse=True)
fig = plt.figure(figsize=(7,7))
# 使用 hspace和wspace参数设置子图间距
gs = GridSpec(4, 4, figure=fig, hspace=0.1, wspace=0.1)
# 主散点
ax_main = fig.add_subplot(gs[1:, :-1])
scatter =ax_main.scatter(df['sepal_length'], df['sepal_width'], c=unique, cmap='Set1', s=40, edgecolors='k')
ax_main.set_xlabel('Sepal Length (cm)')
ax_main.set_ylabel('Sepal Width (cm)')
ax_main.grid(True, linestyle='--', alpha=0.3)
# 上方直方图
ax_top = fig.add_subplot(gs[0, :-1], sharex=ax_main)
ax_top.hist(df['sepal_length'], bins=15, color='tab:gray', alpha=0.7)
ax_top.tick_params(axis='x', labelbottom=False)
# 右侧直方图
ax_right = fig.add_subplot(gs[1:, -1], sharey=ax_main)
ax_right.hist(df['sepal_width'], bins=15, orientation='horizontal', color='tab:gray', alpha=0.7)
ax_right.tick_params(axis='y', labelleft=False)
# 创建图例 - 确保颜色对应
# 使用散点图的to_rgba方法
legend_elements = [
Patch(
facecolor=scatter.to_rgba(i), # 用散点图自带方法获取准确颜色
edgecolor='black',
label=label
)
for i, label in enumerate(labels)
]
# 添加图例
ax_main.legend(handles=legend_elements, loc='upper right', title='Iris Species')
plt.show()
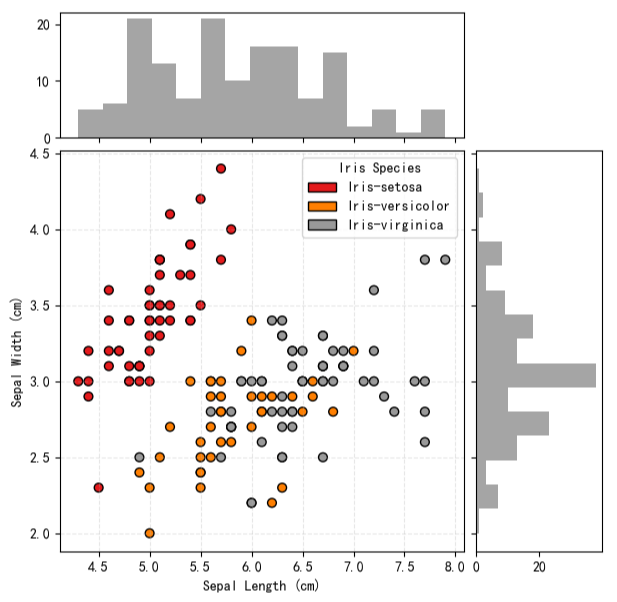
-
使用seaborn:
seaborn 则可通过 jointplot () 函数一键生成。
import seaborn as sns
# 创建jointplot
g = sns.jointplot(
data=df,
x='sepal_length',
y='sepal_width',
hue='class', # 按种类区分颜色
palette={'Iris-setosa': 'red', 'Iris-versicolor': 'green', 'Iris-virginica': 'blue'},
height=8,
alpha=0.7,
edgecolor='k',
linewidth=0.5,
)
# 中心散点图添加网格
g.ax_joint.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
可视化结果如下图所示:
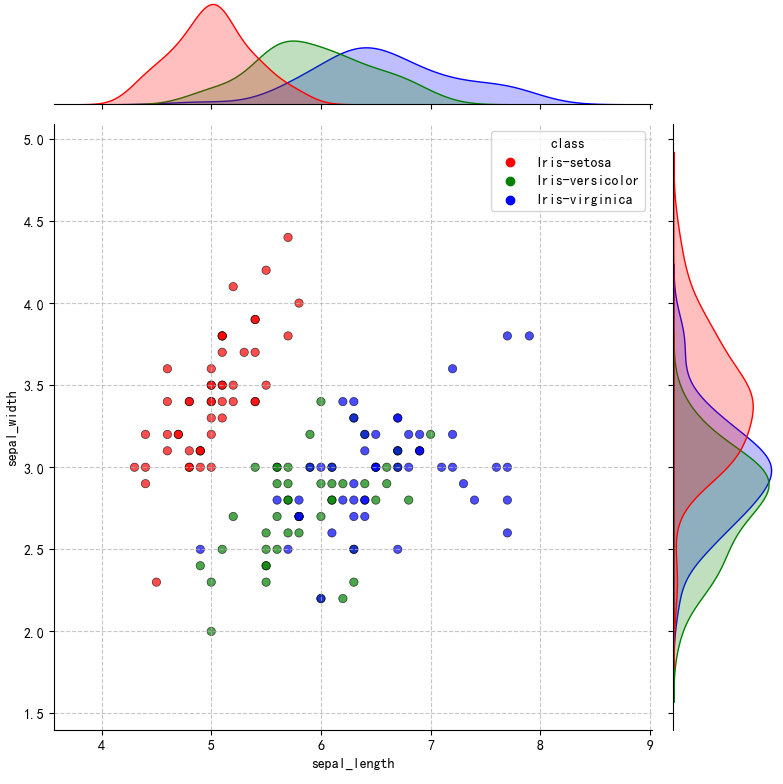
更多内容可以前往官网查看:
https://matplotlib.org/stable/


本篇文章来源于微信公众号: 码农设计师
